Indholdsfortegnelse
En outlier er en værdi, der er væsentligt højere eller lavere end de fleste af værdierne i dine data. Når du bruger Excel til at analysere data, kan outliers skæve resultaterne. For eksempel kan gennemsnittet af et datasæt virkelig afspejle dine værdier. Excel indeholder et par nyttige funktioner til at hjælpe med at administrere dine outliers, så lad os tage et kig.
Et hurtigt eksempel
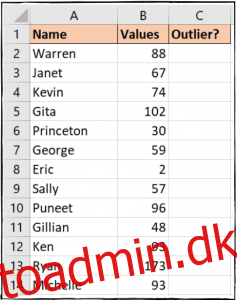
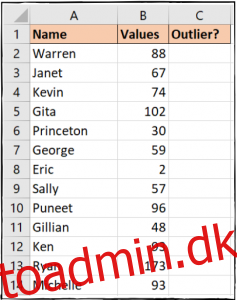
På billedet nedenfor er afvigelserne rimeligt nemme at få øje på – værdien af to tildelt til Eric og værdien af 173 tildelt til Ryan. I et datasæt som dette er det nemt nok at få øje på og håndtere disse outliers manuelt.
I et større datasæt vil det ikke være tilfældet. Det er vigtigt at være i stand til at identificere outliers og fjerne dem fra statistiske beregninger – og det er det, vi skal se på, hvordan man gør i denne artikel.
Sådan finder du outliers i dine data
For at finde outliers i et datasæt bruger vi følgende trin:
Beregn 1. og 3. kvartil (vi taler om, hvad de er om lidt).
Evaluer interkvartilområdet (vi vil også forklare disse lidt længere nede).
Returner de øvre og nedre grænser for vores dataområde.
Brug disse grænser til at identificere de afsidesliggende datapunkter.
Celleområdet til højre for datasættet, der ses på billedet nedenfor, vil blive brugt til at gemme disse værdier.
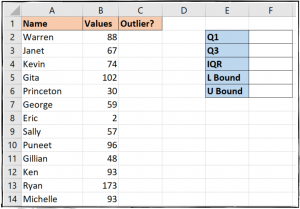
Lad os komme igang.
Trin et: Beregn kvartilerne
Hvis du deler dine data op i kvartaler, kaldes hvert af disse sæt en kvartil. De laveste 25 % af tallene i området udgør 1. kvartil, de næste 25 % 2. kvartil og så videre. Vi tager dette skridt først, fordi den mest udbredte definition af en outlier er et datapunkt, der er mere end 1,5 interkvartilintervaller (IQR’er) under 1. kvartil og 1,5 interkvartilintervaller over 3. kvartil. For at bestemme disse værdier skal vi først finde ud af, hvad kvartilerne er.
Excel giver en KVARTIL-funktion til at beregne kvartiler. Det kræver to stykker information: arrayet og quart.
=QUARTILE(array, quart)
Arrayet er rækken af værdier, som du evaluerer. Og kvartilen er et tal, der repræsenterer den kvartil, du ønsker at returnere (f.eks. 1 for 1. kvartil, 2 for 2. kvartil og så videre).
Bemærk: I Excel 2010 udgav Microsoft funktionerne QUARTILE.INC og QUARTIE.EXC som forbedringer af QUARTILE-funktionen. QUARTILE er mere bagudkompatibel, når du arbejder på tværs af flere versioner af Excel.
Lad os vende tilbage til vores eksempeltabel.

For at beregne 1. kvartil kan vi bruge følgende formel i celle F2.
=QUARTILE(B2:B14,1)
Når du indtaster formlen, giver Excel en liste over muligheder for quart-argumentet.
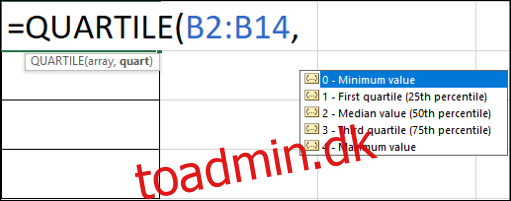
For at beregne den 3. kvartil kan vi indtaste en formel som den forrige i celle F3, men bruge en treer i stedet for en en.
=QUARTILE(B2:B14,3)
Nu har vi kvartildatapunkterne vist i cellerne.
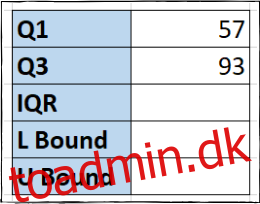
Trin to: Evaluer interkvartilområdet
Interkvartilområdet (eller IQR) er de mellemste 50 % af værdierne i dine data. Den beregnes som forskellen mellem 1. kvartilværdi og 3. kvartilværdi.
Vi vil bruge en simpel formel i celle F4, der trækker den 1. kvartil fra den 3. kvartil:
=F3-F2
Nu kan vi se vores interkvartilinterval vist.
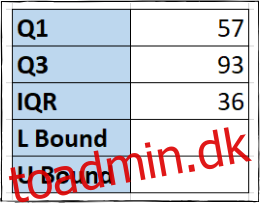
Trin tre: Returner den nedre og øvre grænse
De nedre og øvre grænser er de mindste og største værdier af det dataområde, vi ønsker at bruge. Alle værdier, der er mindre eller større end disse bundne værdier, er outliers.
Vi beregner den nedre grænse i celle F5 ved at gange IQR-værdien med 1,5 og derefter trække den fra Q1-datapunktet:
=F2-(1.5*F4)
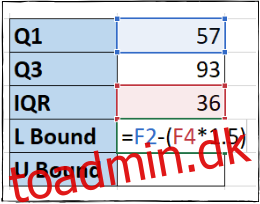
Bemærk: Klammerne i denne formel er ikke nødvendige, fordi multiplikationsdelen vil beregne før subtraktionsdelen, men de gør formlen lettere at læse.
For at beregne den øvre grænse i celle F6, multiplicerer vi IQR med 1,5 igen, men denne gang føjes den til Q3 datapunktet:
=F3+(1.5*F4)
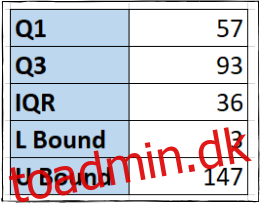
Trin fire: Identificer outliers
Nu hvor vi har sat alle vores underliggende data op, er det tid til at identificere vores afsidesliggende datapunkter – dem, der er lavere end den nedre grænseværdi eller højere end den øvre grænseværdi.
Vi vil bruge ELLER funktion for at udføre denne logiske test og vise de værdier, der opfylder disse kriterier, ved at indtaste følgende formel i celle C2:
=OR(B2$F$6)
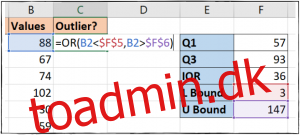
Vi kopierer derefter denne værdi ind i vores C3-C14-celler. En TRUE værdi angiver en outlier, og som du kan se, har vi to i vores data.
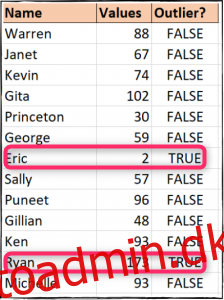
Ignorer outliers ved beregning af middelgennemsnittet
Ved at bruge QUARTILE-funktionen kan vi beregne IQR og arbejde med den mest udbredte definition af en outlier. Men når man beregner middelgennemsnittet for en række værdier og ignorerer outliers, er der en hurtigere og nemmere funktion at bruge. Denne teknik vil ikke identificere en outlier som før, men den vil give os mulighed for at være fleksible med, hvad vi kan betragte som vores outlier-del.
Funktionen vi skal bruge hedder TRIMMEAN, og du kan se syntaksen for den herunder:
=TRIMMEAN(array, percent)
Matrixen er det interval af værdier, du ønsker at gennemsnittet. Procenten er procentdelen af datapunkter, der skal udelukkes fra toppen og bunden af datasættet (du kan indtaste det som en procentdel eller en decimalværdi).
Vi indtastede formlen nedenfor i celle D3 i vores eksempel for at beregne gennemsnittet og udelukke 20% af outliers.
=TRIMMEAN(B2:B14, 20%)
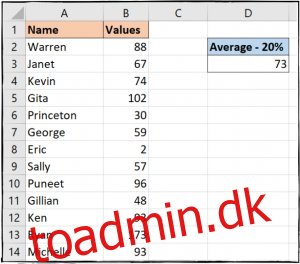
Der har du to forskellige funktioner til håndtering af udliggere. Uanset om du vil identificere dem for nogle rapporteringsbehov eller udelukke dem fra beregninger såsom gennemsnit, har Excel en funktion, der passer til dine behov.